
Contidos:
Este tema trata de exercicios con decibelios, que son as unidades que se utilizan en telecomunicacións e radiocomunicacións para medir potencias, voltaxes e ganancias en lugar de watios, voltios e ganancias unitarias.
Comecemos por ver en que se utilizan os decibelios:
Repara en que 0dBx equivale a unha unidade de “x” no sistema natural.
Como ves, traballaremos con voltaxes e potencias, que se relacionan mediante $P=\frac{V^{2}}{Z}$ (só en unidades naturales, non en decibelios).
“Z” é a impedancia característica do sistema (antenas, liñas, amplis…). En ICT1 e en redes WAN coaxiais se traballa con Z=75Ω. En todo o resto de radiocomunicacións (Wi-Fi, telefonía, naval…) se traballa a Z=50Ω.
En radiocomunicacións, a maior parte do traballo consiste en seguir o camiño polo que circula un sinal eléctrico, case sempre de ou ata unha antena (recepción/transmisión) e ver como vai evolucionando o sinal usando unidades en decibelios.

A corrente eléctrica flúe no sentido no que apunta o triángulo, que é o símbolo do amplificador. Neste caso ten ganancia 2, polo cal a potencia de saída será dúas veces a de entrada. No primeiro exemplo inxectamos un sinal de 4W de potencia e no segundo 5,5W. Observa como as saídas aumentan o nivel de entrada segundo a ganancia de amplificación:
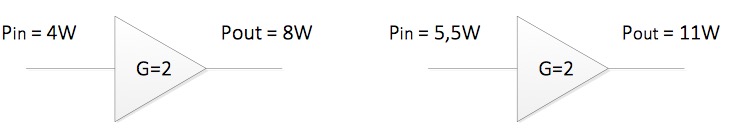
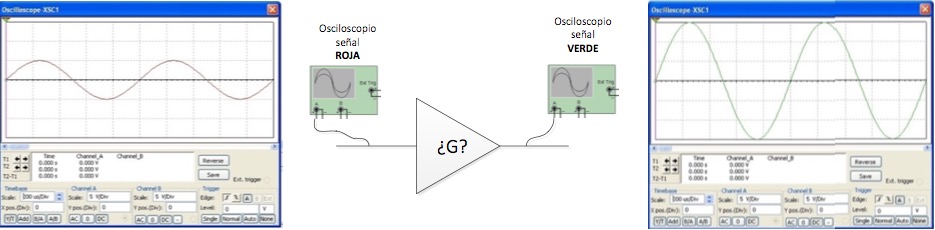
A principal vantaxe dos decibelios é que nos permite deixar de operar con multiplicacións e divisións para pasar a traballar con sumas e restas (máis fácil).
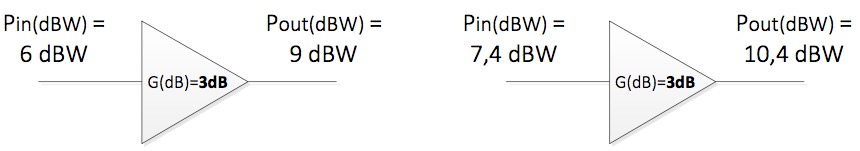
Así:
$$ P_{out}(dBW) = G(dB) +Pin(dBW) \Longleftrightarrow{} G(dB) = P_{out}(dBW) - P_{in}(dBW)$$Como hai cambios respecto o apartado anterior. O signo de multiplicación cambia polo de suma e o de división polo de resta.
En principio non parece que aporte moito, pero se complicamos os circuítos, os cálculos se volven moito máis rápidos.


O resultado é o mesmo. Comprobamos que $10\cdot \log {31,6W} = 16dBW$
Táboa de conversións:
| de sistema internacional a dB | de dB a sistema internacional | ||
|---|---|---|---|
| Ganancias | Ganancia en potencia (unitaria e en dB) |
$$G(dB)=10\cdot \log{G_{P}}=20\cdot\log{G_{V}}$$ | $$G_{P}=10^{\frac{G(dB)}{10}}=\frac{P_{out}}{P_{in}}$$ |
| Ganancia en voltaxe (unitaria e en dB) |
$$G_{V}=10^{\frac{G(dB)}{20}}=\frac{V_{out}}{V_{in}}$$ | ||
| Magnitudes físicas | Voltaxe | $$V(dBV) = 20\cdot\log{V(V)}$$ | $$V(V) =10^{\frac{V(dBV)}{20}}$$ |
| $$V(dBµV) = 20\cdot\log{V(µV)}$$ | $$V(µV) =10^{\frac{V(dBµV)}{20}}$$ | ||
| Potencia | $$P(dBW) = 10\cdot\log{P(W)}$$ | $$P(W) =10^{\frac{P(dBW)}{10}}$$ | |
| $$V(dBm) = 10\cdot\log{P(mW)}$$ | $$P(mW) =10^{\frac{P(dBm)}{10}}$$ | ||
Na columna da esquerda, o número 10 que multiplica ó logaritmo é debido a que as unidades son “decibelios” (décima parte do belio). “Belio” é en horno a Alexander Graham Bell. Ás veces non é 10 senón 20 ($20=10\cdot2$). Iso é debido á Lei de Watt:
$$P=V\cdot I=\frac{V^2}{Z}=I^2\cdot Z$$Estes expoñentes “ó cadrado” saen da operación logaritmo multiplicando. É un proceso un pouco complexo, pero non é necesario entendelo:
$$G(dB)=10\cdot\log\frac{P_{out}}{P_{in}}= 10\cdot\log\frac{\frac{V^2_{out}}{Z}}{\frac{V^2_{in}}{Z}}=10\cdot\log\frac{V^2_{out}}{V^2_{in}}= 10\cdot\log(\frac{V_{out}}{V_{in}})^2=10\cdot2\cdot\log\frac{V_{out}}{V_{in}}=20\cdot\log\frac{V_{out}}{V_{in}}$$Detectas algo interesante nos números resultantes?
| Ganancia unitaria e magnitudes en sistema internacional |
Operacións en decibelios | |
|---|---|---|
| Amplificación | Multiplicar (X) | Sumar (+) |
| Atenuación | Dividir (÷) | Restar (-) |
Comprobacións para a equivalencia $"\cdot 2 ≈ +3dB"$:
| $G=2;\, G(dB)=10\cdot\log{2}=+3dB$ | $G=\frac{1}{2}=0,5;\, G(dB)=10\cdot\log{\frac{1}{2}}=-3dB$ |
|---|---|
| $G=4;\, G(dB)=10\cdot\log{4}=+6dB$ | $G=\frac{1}{4}=0,25;\, G(dB)=10\cdot\log{\frac{1}{4}}=-6dB$ |
| $G=8;\, G(dB)=10\cdot\log{8}=+9dB$ | $G=\frac{1}{8}=0,125;\, G(dB)=10\cdot\log{\frac{1}{8}}=-9dB$ |
Comprobacións para a equivalencia $"\cdot 10 = +10dB"$:
| $G=10;\, G(dB)=10\cdot\log{10}=+10dB$ | $G=\frac{1}{10}=0,1;\, G(dB)=10\cdot\log{\frac{1}{10}}=-10dB$ |
|---|---|
| $G=100;\, G(dB)=10\cdot\log{100}=+20dB$ | $G=\frac{1}{100}=0,01;\, G(dB)=10\cdot\log{\frac{1}{100}}=-20dB$ |
| $G=1000;\, G(dB)=10\cdot\log{1000}=+30dB$ | $G=\frac{1}{8}=0,001;\, G(dB)=10\cdot\log{\frac{1}{1000}}=-30dB$ |
Se analizamos os datos anteriores, veremos que unha ganancia que amplifica sempre vai ser maior de 1 en unitaria e maior de 0 en decibelios. Polo contrario, unha atenuación valerá entre 0 e 1 en unitaria e un valor negativo en dB:
| Atenuación e valores en voltios/watios menores que a unidade de referencia |
Amplificación e valores en voltios/watios maiores da unidade que a referencia |
|
|---|---|---|
| Ganancia unitaria e operacións en sistema internacional |
De 0 a 1 | De 1 a ∞ |
| Operacións en decibelios | Valores negativos | Valores positivos |
Tamén se demostra que:
Nos módulos de ciclo superior, se poden usar outros trucos para pasar entre distintas unidades. Por exemplo:
$$P(dBm)=P(dBW)+30dB$$ $$V(dBµV)=P(dBV)+120dB$$O anterior é lóxico se pensamos que para pasar de W a mW hai que multiplicar por 1000 (+30dB). No caso dos voltios, multiplicamos por 1000000 (+120dB, por estar en voltios)
Cando estamos no sistema internacional podemos pasar de voltios a watios usando a Lei de Watt $"P=V^{2}/Z"$. A equivalencia en decibelios é a seguinte:
$$P(dBm)=V(dBµV)-90dB-10\cdot\log{Z(Ω)}$$Isto é moi útil en ICT, xa que ahí se traballa fundamentalmente en dBµV pero o ruído térmico se calcula inicialmente en W.
Resumindo:
| G(dB) | G(W/W) (unitaria) |
G(dB) | G(W/W) (unitaria) |
|---|---|---|---|
| 3 dB | 1 | ||
| 100 | 0,5 | ||
| 200 | 12 dB | ||
| -17 dB | -20 dB |
(repara que á ganancia unitaria ás veces se lle poñen as unidades en W/W e á unitaria en voltaxe en V/V)
Pídese:

Son interesantes tamén os problemas do final do tema 1 do libro “Televisión y Radio Analógica y Digital” de Televés.
Realiza medicións de potencia/voltaxe nunha instalación coaxial. Deberás utilizar un medidor de campo (se o fas nunha instalación de radio/TV/SAT) ou ben un analizador de redes2 (se mides o cableado coaxial dunha Wi-Fi ou trunking). A opción máis sinxela é a primeira, xa que de seguro terás unha maqueta dunha ICT no teu centro:

Pasos para realizar a práctica:
Entrega un documento en formato PDF na páxina da tarefa con fotos e explicacións.
Nas seguintes imaxes podes ver medidas de voltaxe en TDT (esquerda) e de potencia en Wi-Fi (centro e dereita):
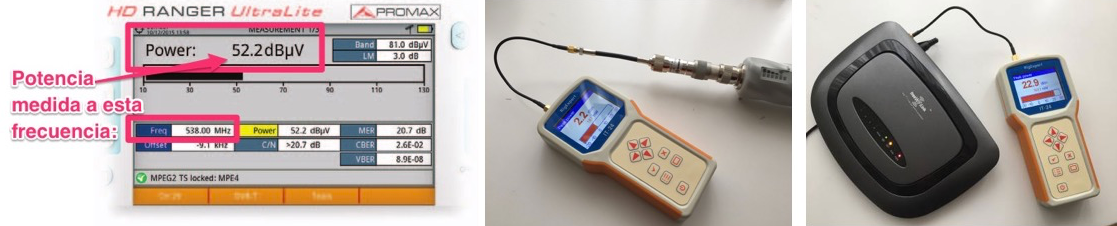
Recomendo que fagas a medida de TDT se non tes coñecementos previos. Enlace a vídeo explicativo. No centro atoparás compañeiros que che orientarán cos equipos de ICT. As medicións Wi-Fi son unha opción máis avanzada que require material que probablemente non teñas.
Entrega en formato PDF na páxina da tarefa. Dúbidas no foro de consultas. Non esquezas facer o cuestionario deste tema.
Creado para G1701016 – “Radiocomunicacións prácticas” por Daniel Ríos Suárez
 Licenciado baixo a Licenza Creative Commons Recoñecemento Compartir igual 4.0
Licenciado baixo a Licenza Creative Commons Recoñecemento Compartir igual 4.0
Este curso virtual elaborouse para ser impartido no plan anual de formación do profesorado de FP da Consellería de Cultura, Educación e Ordenación Universitaria, Xunta de Galicia
Quedan fora desta licenza os textos, imaxes, recursos... que manteñen a súa propia licenza, sinalada en cada caso.
Úsanse imaxes e recursos de producción propia, que se publican no Dominio público ou con licenza CC BY-SA, outras de dominio público, con licenza creative commons, GNU... tomados prefentemente de bancos de recursos educativos abertos. Tamén se empregan ---acolléndose ao "Dereito de cita" --- imaxes, e recursos diversos de diferentes páxinas web, e se enlaza a súa licenza ao pé dos propios recursos ou na páxina coa atribución da propiedade intelectual dos ODE empregados, dereitos reservados que manteñen integramente. Se detecta algunha imaxe, recurso... con dereitos reservados, agradecemos nos informe para retirala.