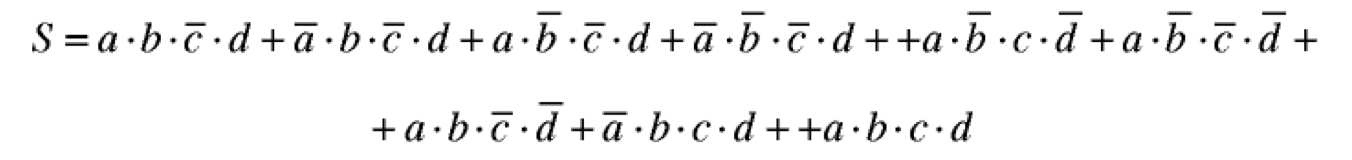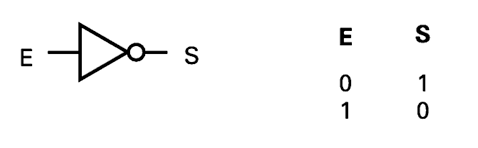
Las puertas lógicas son los elementos constituyentes de los circuitos digitales.
La salida es el complemento de la entrada:
$$ S=\overline{E} $$
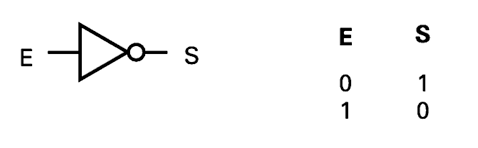
$$ S=A $$

$$ S=A\cdot B $$
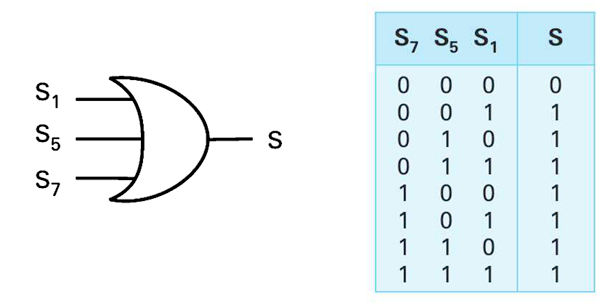
Ejemplo con tres entradas:

$$ S=A+B $$
Ejemplo con tres entradas:
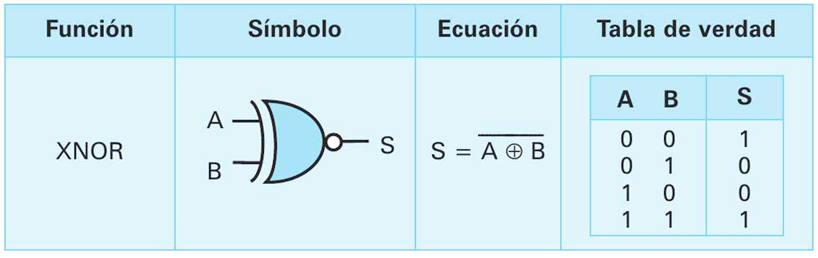
Puerta “OR exclusiva”

$$ S=A\oplus B = A \cdot \bar{B} + B \cdot \bar{A} $$
Si las entradas son iguales, la salida es “0”; si las entradas son distintas, la salida es “1”.
Ejercicio anterior resuelto. Simúlalo en Logisim:

$$ S=\overline{A\cdot B} $$

$$ S=\overline{A+ B} $$

$$ S=\overline{A \oplus B} $$
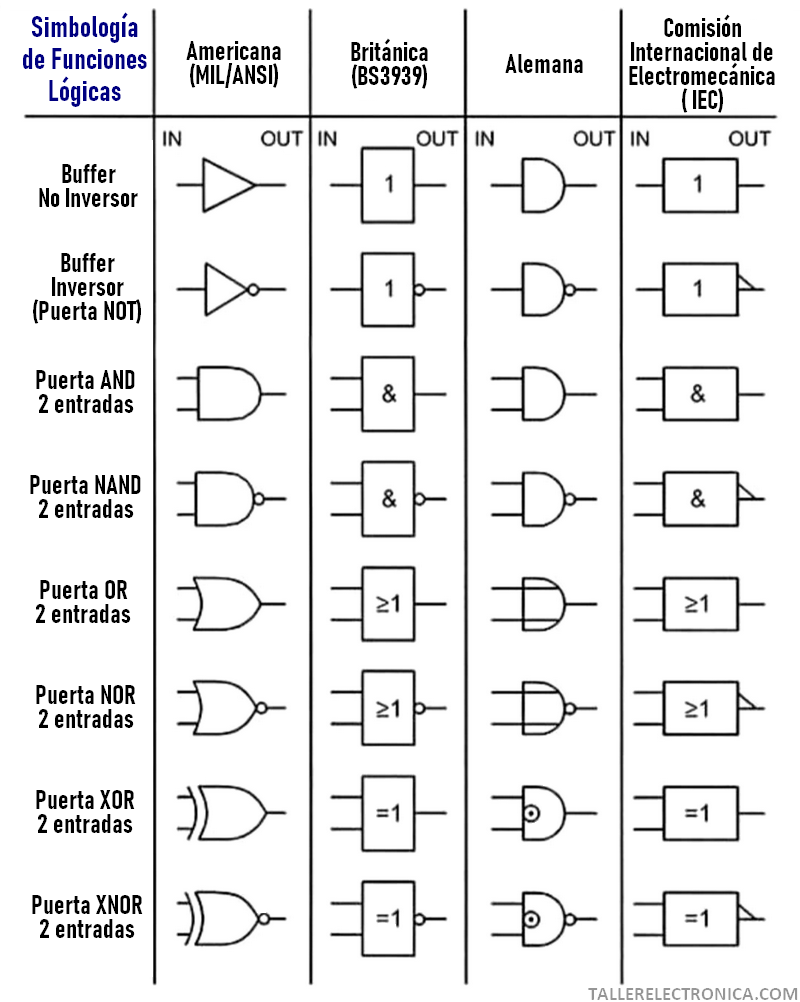
ICs (circuitos integrados, “chips”) de la serie 7400:

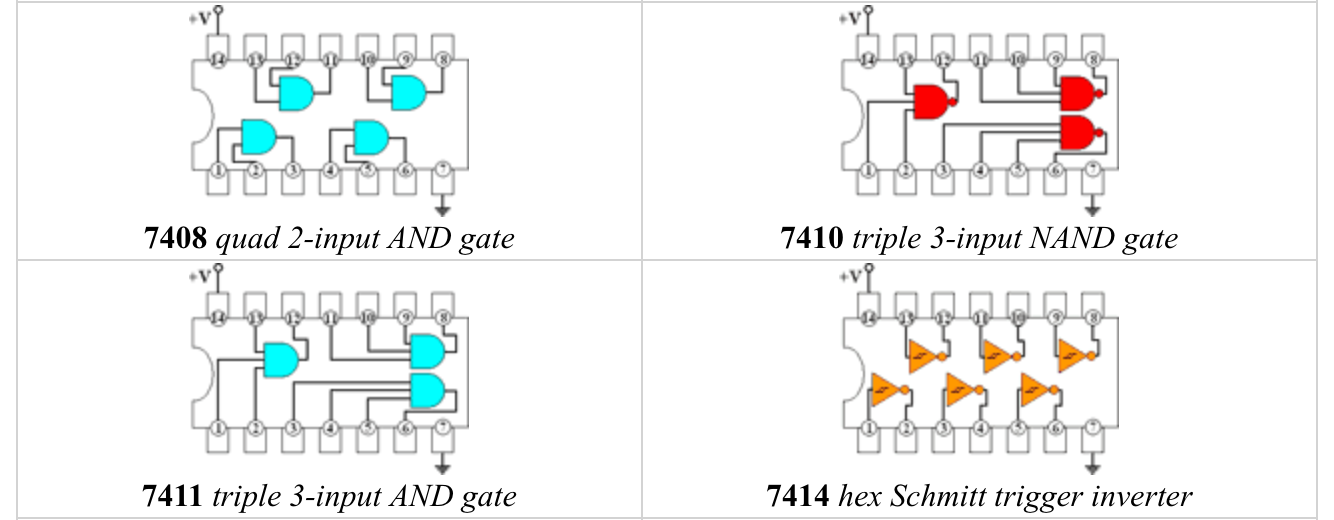

Atención: si les metes tensiones negativas a la entrada, se estropean.
Bajo consumo eléctrico, pero tiempos de respuesta ligeramente más rápidos que en TTL. Míralas en https://es.wikipedia.org/wiki/Serie_4000
Atención: no cuentan con protección antiestática, pueden estropearse con el contacto con las manos.
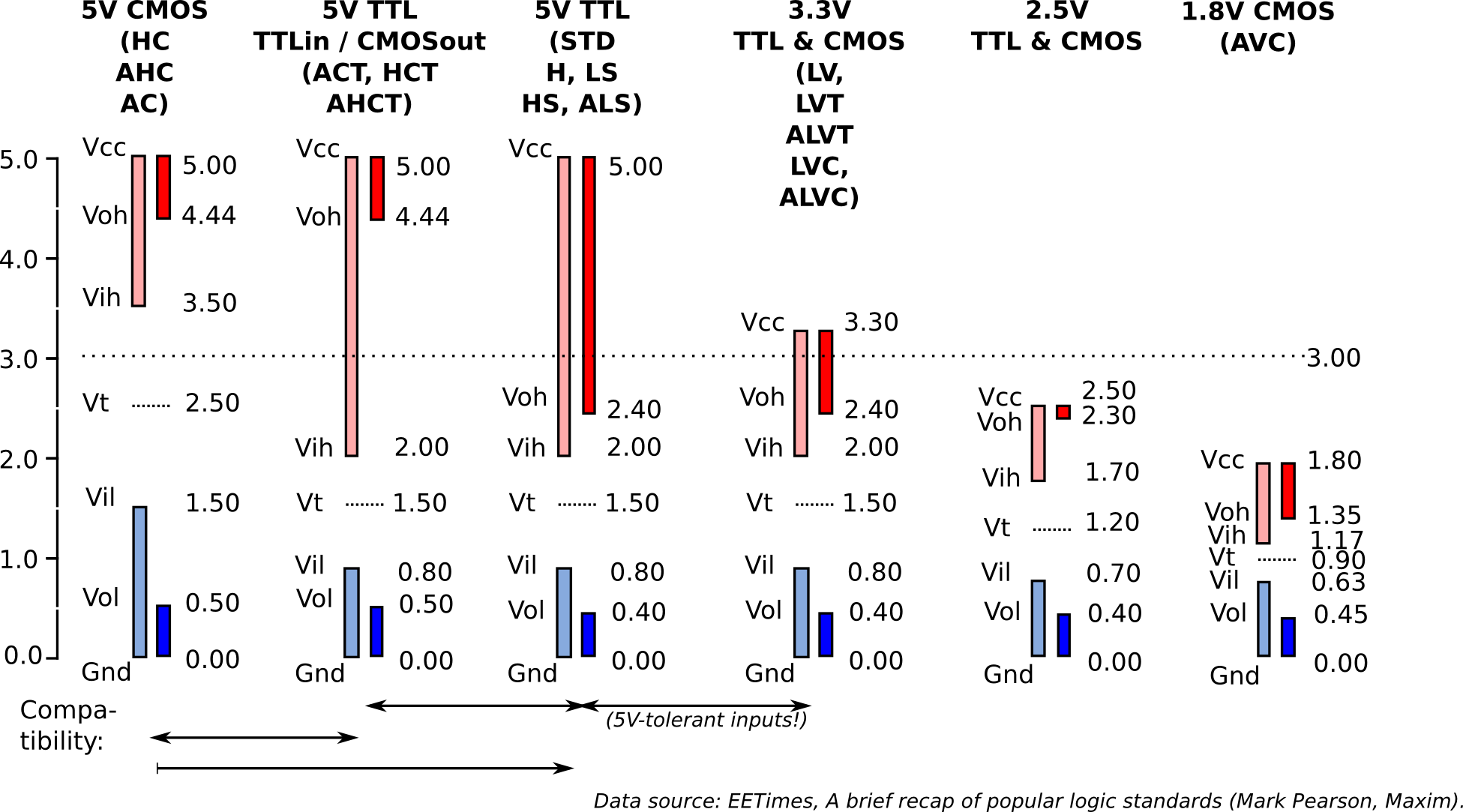
El álgebra booleana permite simplificar circuitos lógicos:
Leyes fundamentales de OR:
$$ A+0=A $$
$$ A+1=1 $$
$$ A+A=A $$
$$ A+\overline{A}=1 $$
Leyes fundamentales de AND:
$$ A\cdot 1=A $$
$$ A\cdot 0=0 $$
$$ A\cdot A=A $$
$$ A\cdot\overline{A}=0 $$
Ley fundamental de NOT:
$$ \overline{\overline{A}}=A $$
Propiedad conmutativa:
$$ A+B= B+A $$
$$ A\cdot B= B \cdot A $$
Propiedad asociativa:
$$ (A+B)+C= A+(B+C)$$
$$ (A \cdot B) \cdot C= A \cdot (B \cdot C)$$
Propiedad distributiva:
$$ A \cdot (B+C) = (A \cdot B) + (A \cdot C)$$
$$ A + (B \cdot C) = (A + B) \cdot (A + C)$$
Estas son las más importantes!!!
$$ \overline{A\cdot B}=\overline{A} + \overline{B} $$
$$ \overline{A+ B}=\overline{A} \cdot \overline{B} $$
Si combinamos con la ley fundamental del NOT, que decía que $ \overline{\overline{A}}=A $, podemos convertir fácilmente sumas en productos y viceversa:
$$ {A+ B}=\overline{\overline{A + B}} = \overline{\overline{A}\cdot \overline{B}} $$
¿No tienes puertas NOR? ¡usa NAND!
$$ {A\cdot B}=\overline{\overline{A \cdot B}} = \overline{\overline{A}+\overline{B}} $$
¿No tienes puertas NAND? ¡usa NOR!
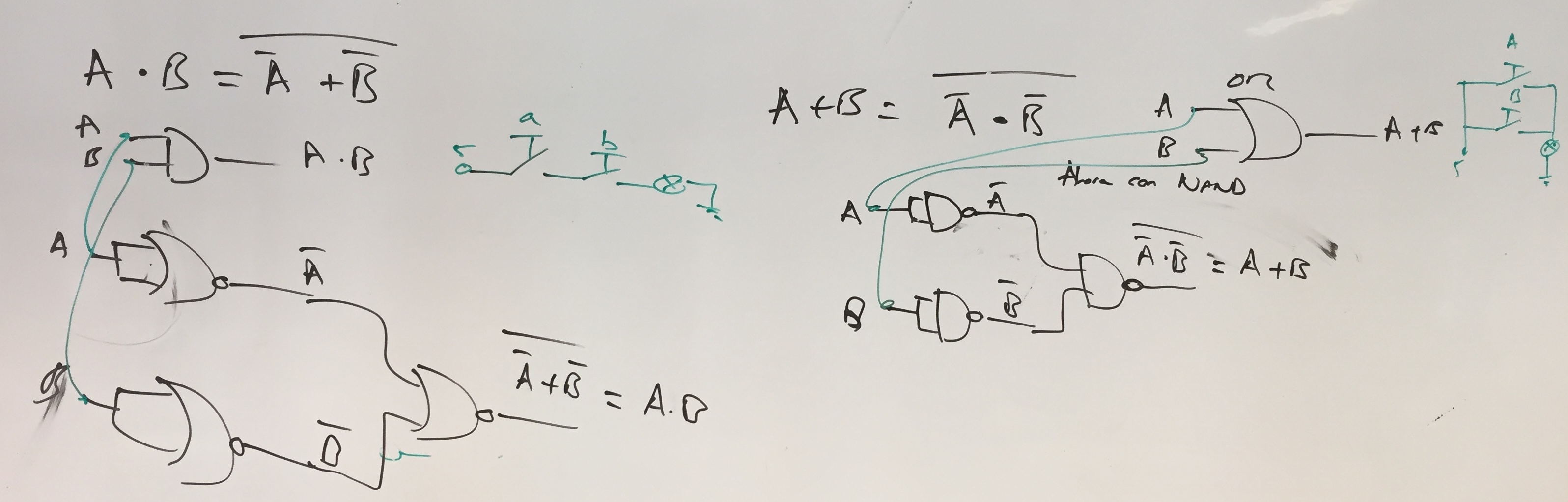
Tenemos entonces dos formas de hacer cada uno de los dos circuitos. Fíjate que las entradas A, B se cortocircuitan para excitar los dos formatos a la vez.
Las leyes de De Morgan permiten resolver cualquier circuito lógico sólo con puertas NAND o bien sólo con puertas NOR. Esto se debe a que estas puertas engloban la función de la AND, de la OR y de la NOT.
Las funciones canónicas son expresiones matemáticas que engloban toda una tabla de verdad. Ofrecen dos posibilidades:
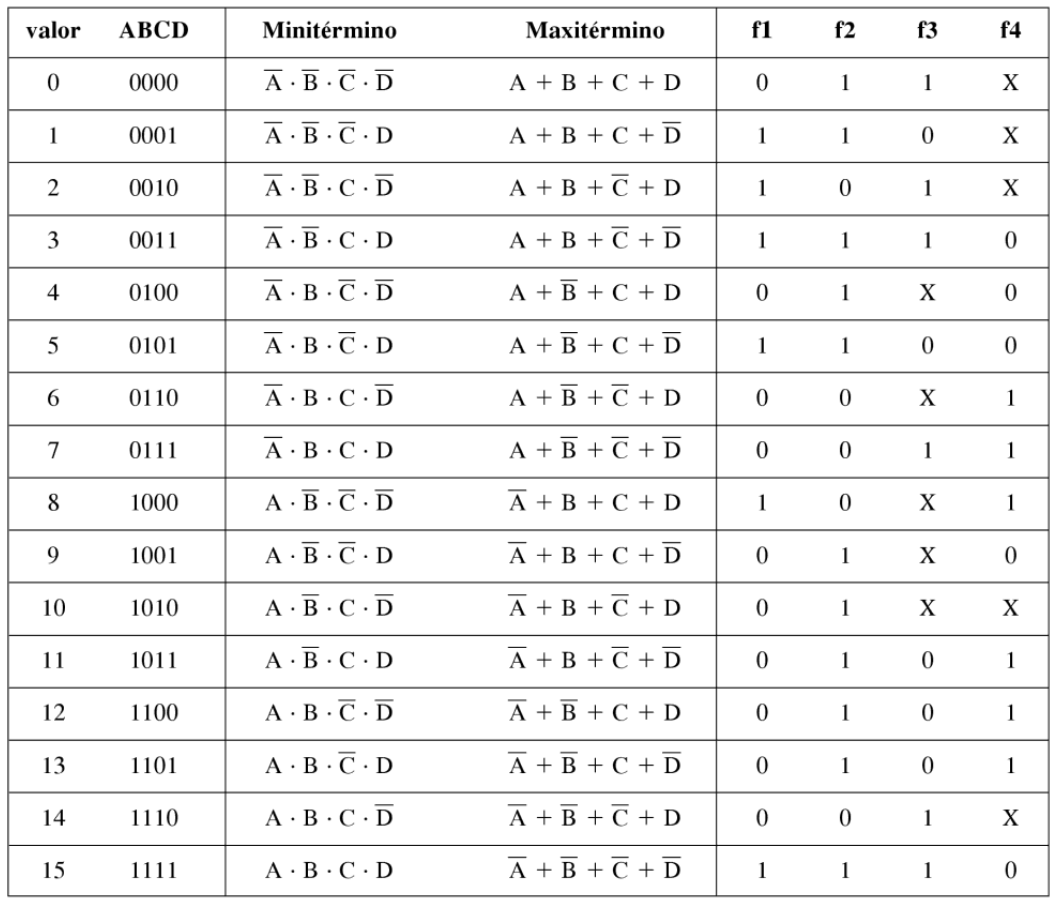
Por ejemplo, dadas las entradas A, B, C, D podemos expresar la salida f1:
$$f1= \overline{A} \cdot \overline{B} \cdot \overline{C} \cdot D + \overline{A}\cdot\overline{B}\cdot C \cdot \overline{D} + \overline{A}\cdot \overline{B} \cdot C \cdot D + \overline{A} \cdot B \cdot \overline{C} \cdot D + A \cdot\overline{B}\cdot \overline{C} \cdot \overline{D} + A \cdot B \cdot C \cdot D $$
$$f1= (A+B+C+D)\cdot (A+\overline{B}+C+D)\cdot (A+ \overline{B}+ \overline{C} + D)\cdot (A+ \overline{B}+ \overline{C}+ \overline{D}) \cdot (\overline{A}+B+C+\overline{D}) \cdot (\overline{A}+B+\overline{C}+D) \cdot (\overline{A}+B+ \overline{C}+ \overline{D})\cdot (\overline{A}+\overline{B}+C+D)\cdot (\overline{A}+ \overline{B}+ C+ \overline{D})+(\overline{A}+ \overline{B}+ \overline{C}+D)$$
Ambas funciones son equivalentes. Usaremos la suma de productos casi siempre.
Las funciones anteriores se podrían simplificar aplicando las propiedades del álgebra de Boole, pero no es rápido ni práctico. En lugar de eso, usaremos la técnica de los mapas de Karnaugh.
Se trata de representar la tabla de verdad en dos dimensiones en la que los bits se ordenen en código Gray.
Una vez representada la tabla, deberás rodear los grupos de bits adyacentes: grupos de 1, 2, 4, 8… (potencias de 2). Siempre la mayor cantidad posible.
Debes entender la tabla como un mapamundi (la tierra es redonda) y por tanto las celdas de los lados son adyacentes, y las de los lados también.
Dos variables de entrada:
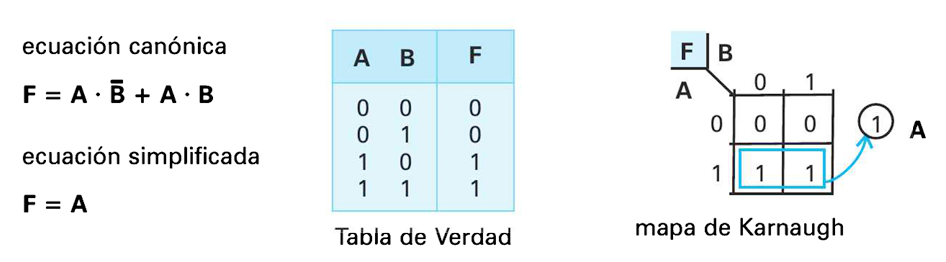
Tres variables de entrada:

Cuatro variables de entrada:

Tenemos tres pulsadores y un grifo. El grifo se activa cuando se pulsan al menos dos de los tres pulsadores.
Y ahora hazlo simplificando:
Ejercicio 1: Escribe la función canónica y simplifica mediante mapas de Karnaugh las siguientes tablas de verdad:
a)

b)

c)

Ejercicio 2: Dibuja la tabla de verdad y simplifica las siguientes funciones canónicas con el método de Karnaugh:
a)
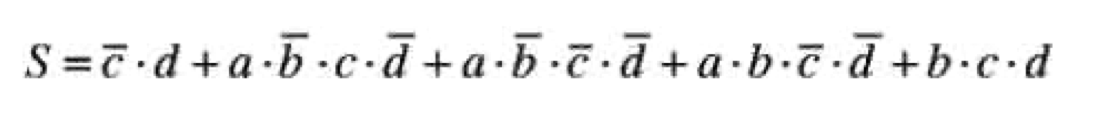
b)